Achille finalmente raggiunge la tartaruga
di Antonio Sparzani

Parlando della presa del pensiero sulla realtà, spero di avervi convinto almeno di una cosa, che per superare, risolvere, capire davvero quello che sembra un paradosso, occorre andargli dentro e spiegarlo con le sue stesse armi: nel caso della storia di Achille e della tartaruga, non basta cioè l’osservazione sperimentale del fatto che voi – ancorché non siate il Piè Veloce – raggiungete facilmente, se volete, qualsiasi tartaruga arranchi davanti ai vostri piedi (in terra, perché in mare con quelle delle Galàpagos, non saprei…), e neppure basta una procedura apparentemente più razionale, e cioè quello che seguirebbe qualsiasi studente di meccanica cui venisse posto il problema così formulato: dato Achille che corre con velocità V e parte da un punto distante a dal punto, davanti a lui, dal quale parte una tartaruga che comincia a correre (si fa per dire) con velocità v nello stesso istante nel quale comincia Achille e ovviamente nella stessa direzione, dopo quanto tempo (se, come si presume, V è maggiore di v) Achille raggiunge la tartaruga e a che distanza dal punto di partenza di Achille? A questo problema qualsiasi studente liceale che sappia i primi elementi di cinematica risponde in minuti quattro che il tempo richiesto è pari a a /(V-v) e che il punto nel quale avviene il sorpasso dista aV / (V-v) dal punto di partenza di Achille.
Ma non è questo il fatto cruciale: se crediamo, almeno un poco, alla coerenza logica del sensato ragionare.
Per rispondere a Zenone occorre dire se e come il suo ragionamento è sbagliato e come invece, anche seguendo correttamente il suo ragionamento, Achille raggiunge la tartaruga esattamente nello stesso momento e nello stesso luogo previsti dallo studente di meccanica.
Qual è il motivo per cui il ragionamento di Zenone sembra concludere che Achille non possa raggiungere la tartaruga? Il motivo è che il ragionamento presuppone infiniti passi e non si possono certo fare infiniti passi in un tempo finito, no? O sì?
Vediamo.
Un modo semplice per convincervi che invece ciò è largamente possibile, basta avere la mente un po’ aperta, ma neanche poi tanto, è il seguente:
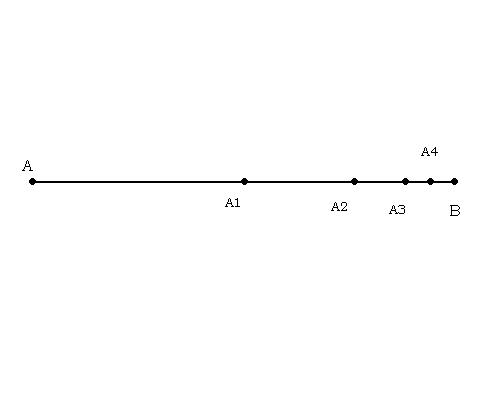
Tutti sapete, e vedete in questa figura, cos’è un segmento AB; anzi sapete anche che contiene tanti punti quanto un’intera retta, cioè aleph, e via dicendo. Allora prendete AB e dividetelo a metà, chiamate A1 il punto di mezzo. Ora considerate la seconda metà delle due ottenute, cioè il segmento A1 B, e dividetelo a metà, ottenendo così il punto di mezzo A2. Analogamente ottenete i punti A3, A4, ecc. dividendo sempre a metà l’ultima metà precedentemente ottenuta.
In questo modo ottenete una successione di infiniti punti (A1, A2, A3, …..) e di infiniti segmenti: (A A1, A1 A2, A2 A3, A3 A4, …); tutti questi segmenti hanno questa proprietà, che sono tutti contenuti nel segmento A B, che tra loro non si sovrappongono (a parte i punti estremi, che non contano nulla) e che sono “tanti quanti” i numeri interi, cioè sono aleph con zero. Ma hanno soprattutto la straordinaria proprietà che la loro somma, somma di infiniti addendi, è – evidentemente – tutta contenuta nel segmento A B, che ha lunghezza finita. Questo esempio geometrico elementare mostra che la somma di infiniti pezzi, purché, come in questo caso, vadano rimpicciolendosi “abbastanza velocemente”, può anche essere finita. Diciamo che la lunghezza di A B sia 1 metro, e supponiamo di esprimere tutte le lunghezze in metri, allora la lunghezza di A A1 è ½, quella di A1 A2 è ¼, quella di A2 A3 è ⅛, e avanti così. Vuol dire che se eseguo la somma ½ + ¼ + ⅛ + ecc. trovo sempre un numero più piccolo di 1, che ha tra l’altro la proprietà di avvicinarsi a 1 quanto voglio io – basta sommare abbastanza tanti addendi.
Allora abbiamo stabilito questo, che la somma di infiniti addendi non è necessariamente infinita, può anche essere finita, dipende se mai da come sono fatti questi “infiniti addendi”. E allora cade il motivo principale di stupore per il paradosso di Achille e la tartaruga, che può venire trattato con gli strumenti dell’analisi ordinaria.
Questo è il punto essenziale, Zenone sbaglia quando conclude, dopo avere astutamente diviso il lasso di tempo nel quale Achille raggiunge la tartaruga in infiniti intervallini, sempre più piccoli, che allora, siccome questi sono infiniti, il raggiungimento non è possibile. L’esempio del segmento fa invece toccare con mano che questa conclusione è assolutamente non necessaria: la somma di infiniti numeri può dare un numero finito.
Rimarrebbe da eseguire esplicitamente il calcolo, seguendo la linea di Zenone, cioè l’astuta suddivisione, calcolo che mostra come anche così si ottengono esattamente gli stessi risultati dello studente di meccanica. Per far questo, occorre dare senso rigoroso a quell’espressione che con tanta leggerezza ho usato, la “somma di infiniti numeri”, e occorre conoscere come si fa a sommare una serie, cosa che qui non faccio, per non appesantire la faccenda e anche perché non saprei come scrivere qui le formule necessarie. Ma le formule, come spesso accade, non sono il cuore del problema: una volta che si sia guardato con l’occhio addestrato il segmento A B, tutto diventa chiaro.
Come ho già detto, Borges si occupa attivamente della questione. Oltre al saggio che già avevo citato, ve n’è un altro, intitolato “La perpetua corsa di Achille e della tartaruga”, nel quale molte delle argomentazioni qui esposte sono accennate, e peraltro borgesianamente trattate. Vi copio, dulcis in fundo, la conclusione di questo saggio:
Sono arrivato al finale della mia notizia, non del nostro cavillare. Il paradosso di Zenone di Elea, come osservò James, è un attentato non solo alla realtà dello spazio, bensì a quella più invulnerabile e sottile del tempo. Aggiungo che l’esistenza in un corpo fisico, la permanenza immobile, lo scorrere di una sera della vita, si allarmano di avventura per colpa sua. Quella decomposizione accade mediante la sola parola infinito, parola (e poi concetto) di spavento che abbiamo generato temerariamente e che una volta ammessa in un pensiero, esplode e lo uccide. (Ci sono altri moniti antichi contro il commercio di una parola tanto perfida: c’è la leggenda cinese dello scettro dei re di Liang, che diminuiva di una metà ad ogni nuovo re; lo scettro, mutilato da dinastie, esiste ancora.) La mia opinione, dopo quelle qualificatissime che ho presentato, corre il doppio rischio di sembrare impertinente e banale. La formulerò, tuttavia: Zenone è incontestabile, a meno di confessare l’idealità dello spazio e del tempo. Accettiamo l’idealismo, accettiamo l’accrescimento concreto di quanto è percepito, e potremo eludere il brulicare di abissi del paradosso.
Ritoccare il nostro concetto dell’universo, per quel pezzettino di tenebra greca?, domanderà il mio lettore.
(J. L. Borges, Tutte le opere, vol. I, Meridiani Mondadori, Milano 1984, pp. 384-85).


All the arguments of Zeno depend upon that a continuum has ultimate parts. But a continuum is precisely that, every part of which has parts, in the same sense. Hence, he makes out his contradictions only by making a self-contradictory supposition. In ordinary and mathematical language, we allow ourselves to speak of such parts -points- and whenever we are led into contradiction thereby, we have simply to express ourselves more accurately to resolve the difficulty (CP 5.335).
e quante lettere dovette scrivere Charles Sanders Peirce a William James
e quanti argomenti elaborare
nulla da fare: proprio non capiva.
Puoi dire al pie’ veloce Achille di fare un salto anche alle Galapagos e di raggiungere il lonesome George, il solitario ultimo esemplare delle sua specie, per fargli un po’di compagnia? Grazie.
@ pagliardi
difficile chiedere a Peirce di “elaborare” qualcosa. Troppo impegnato nell’ usare la sua “intuizione” per identificare, senza averlo mai visto, il ladro del suo orologio d’oro. Dopo aver chiesto all’ufficiale di bordo di portargli davanti tutti i camerieri “negri” della nave su cui aveva viaggiato.
@soldato blu
liberissimo di non conoscere peirce
dopo l’ostracismo e l’emarginazione da parte del mondo accademico di allora;
data la difficoltà a seguire o solo a rintracciare il suo pensiero nella mole di scritti in gran parte inediti
uno in più non fa la differenza
però l’accusa è originale
tuttavia un grossolano abbaglio
@ pagliardi
infatti non ho preteso di conoscere Peirce, nè di aver fatto qualcosa perché l’accademia non lo riconoscesse nel suo valore [la stessa accademia si offenderebbe a vedere il suo nome associato al mio].
In questi post il mio compito è fare, bene, la parte dell’ignorante.
Ho riportato, soltanto, un aneddoto raccontato da lui stesso, vantandosene, e riportato in:
PEIRCE CHARLES S., Opere, Bompiani, Il pensiero occidentale, 2003.
Oltre tutto l’orologio non era suo, ma della Guardia Costiera degli Stati Uniti, che glielo aveva affidato, in quanto Peirce partecipava allora, come Poincaré, a quella grande impresa internazionale ottocentesca per la determinazione delle longitudini.
Del suo pensiero, ammetto, non ho capito nulla, come James, che invece mi sembra di aver capito un po’ di più.
Come invece, ancora , non capisco da cosa sono rimasto abbagliato.
interssante ciò che dice sparzani, che è poi quel che aveva detto più in breve peirce, ma io trovo più acuto quel che dice borges, che è poi quel che aveva detto più in breve zenone. in realtà, risolvere matematicamente o logicamente il paradosso, è solo spostarlo in un’altra area percettiva. ad es. affermando che “la somma di infiniti pezzi, purché, come in questo caso, vadano rimpicciolendosi “abbastanza velocemente”, può anche essere finita”. non resta paradossale il rimpicciolimento, non viola il principio di identità? per farla breve cito un paradosso di wittgenstein: come possiamo affermare che 2+2=4? se un diavoletto, mentre eseguiamo l’operazione, aggiuge un’unità, non fa forse 5? in tal senso, che achille raggiunge la tartaruga, non è un paradosso ma la verità. essa la raggiunge solo nella nostra rappresentazione, ma questa rappresentazione dipende da una serie di assunzioni arbitrarie, e abitudinarie, avrebbe detto peirce. c’è un livello, antecedente lo spazio e il tempo, a cui achille non raggiunge mai la tartaruga. dire questo, obietterà sparzani, è negare che esista una realtà obiettiva, achille e tartaruga inclusi. è proprio questa la verità a cui il varco del paradosso ci voleva far accedere, è questo l’abisso in cui ci voleva far sprofondare.
Il sofisma di Zenone è per sua natura ingannatorio. Se l’infinito è per definizione immisurabile, la misurazione di distanze (quelle percorse dalla tartaruga o da un atomo o da un razzo interstellare) non può essere infinita. Se all’infinito compete natura di astrazione (formulazione ideale non percepibile ai sensi), ciò che è percepibile ai sensi esula da tale formulazione. Infiniti sono perciò i numeri (in positivo o in negativo), finiti sono necessariamente gli spazi fisici misurabili (in aumento o in diminuzione) e perciò percepibili. L’astrazione, non lo spazio fisico, è infinitamente divisibile. Di ciò è prova il tempo, astrazione la cui misurazione (e il cui movimento) è accettata come umano artificio. Cito ancora da Borges, che a sua volta cita Bergson: “si può ben dividere un oggetto, ma non un atto”.
p.s. Qualcuno parla del “freddo ragionare di Borges” per sminuirne gli esiti come scrittore. Sparzani ed altri, fortunatamente, si scaldano anche con questo.
In un piano x/y l’area sottesa da una curva f(x), compresa in un intervallo finito a-b disposto lungo l’asse x, sarebbe immisurabile se non la dividessimo in infiniti rettangolini di altezza f(x) e larghezza infinitesima dx diversa da zero. Va da sè che la somma degli infiniti dx è pari alla lunghezza, finita, dell’intervallo a-b.
Esiste forse una risultanza eccedente quando una misura infinita si porta ad una misura reale, dove l’eccesso è quello di una misura materiale. Se questa risultanza fosse vera all’infinito, il paradosso di Zenone sia pensato, sia sperimentato con mezzi fisici sarebbe valido? Forse sì. Si può considerare la somma dei numeri da uno a cento, e la formula ad essa relativa, in relazione ad una somma di solidi da uno a cento, e vedere che c’è quest’eccedenza nel contesto della materia; quindi l’infinito genera l’eccedenza della materia. Urca.
@niky lismo
“Qualcuno parla del “freddo ragionare di Borges” per sminuirne gli esiti come scrittore. Sparzani ed altri, fortunatamente, si scaldano anche con questo.”
oh bè, di recente mi è capitato pure di leggere l’affermazione di uno “scrittore” italiano che preferiva tolkien a borges…
cmq è bello rileggere borges, soprattutto ora che non ho più neanche un suo libro, e bravo sparz, sempre chiaro e lucido.
zenone trova una frattura tra il mondo e la sua concepibilità…
…come se una volta dimostrato matematicamente che una somma “infinita” di numeri può dare una quantità finita, la questione si potesse chiudere lì.
…il pensiero umano è un prodotto della realtà.
…è “realtà che si pensa” senza disporre di un punto “esterno” su cui fare leva.
…tutto è disperatamente interno a sé stesso, per potersi chiamare davvero conoscenza.
…ehm …mi pare.
La via per uscire dal paradosso è l’amore. Amore che è in sé, e che nello stesso tempo è un punto esterno a sé. Così, come quando ci si innamora, che si sposta il punto centrale della propria vita, e anche quando per primo un altro essere umano ci ama senza che glielo abbiamo chiesto, come un riflesso di un amore infinito.
pierinescamente, devo far notare a sparzani che le tartarughe delle galapagos sono terrestri e sono le più grandi e le più vecchie che esistano: melville dice delle retate di tartarughe che facevano le baleniere quando approdavano su quelle isole: scorte di carne fresca che restava viva per mesi sul ponte delle navi, in attesa di essere uccisa e mangiata: se avessero saputo del paradosso di zenone dove si contemplava la loro irraggiungibilità avrebbero riso amaramente.
io sono sicuro che se Sparzo mi fa una due tre quattro cento ripetizioni di matematica e fisica, non farò più il mio sogno ricorrente in cui devo rifare la maturità (scientifica) con il relativo cauchemardesque esame scritto
effeffe
@tash nelle isole Galàpagos vive la testuggine marina, cosa che mi testimonia sia un mio amico che c’è stato e le ha viste, sia, ad esempio, questo sito. Molto interessante quanto dici invece nel primo commento sull’impossibilità di uno “sguardo dall’esterno” sul mondo, che peraltro nulla toglie alla soluzione, interna al mondo, di un paradosso anch’esso interno al mondo.
A te, effeffe, dò lezioni di math e phys quando vuoi, con apposito Gutturnio, purché mi porti al castello di Venaria a vedere i tesori sommersi d’Egitto.
Quanto alla faccenda del paradosso del nostro amico di Elea, invito sommessamente a sorvegliare il linguaggio che si usa: ovvero: accertarsi di avere in mente abbastanza chiaramente il senso delle parole che si scrivono, non faccio esempi, ma il rischio di dire cose non ben definite incombe ai comuni mortali e quindi anche ai fisici, e agli scienziati in genere.
Certo la via indicata da Topo Gigio è attraente più di altre (La via per uscire dal paradosso è l’amore.) e di questo passo si può andare — peraltro assai piacevolmente — per rane.
Sottolineo solo un’ultima volta che il paradosso è sparito, il paradosso era originato da una assai peculiare maniera di dividere il tempo (finito) del raggiungimento in infiniti intervallini, cosa che si può anche fare, naturalmente, pur di sapere che questa infinita suddivisione non fa diventare infinita la lunghezza dell’intervallo che si è suddiviso.
Questa è una novità, ho sempre saputo che le tartarughe giganti simbolo delle galapagos sono tartarughe di terra, e che anzi si trovano bene soprattutto al secco e possono stare senza bere per periodi lunghissimi.
Avranno delle sorelle marine che incrociano in quei mari.
mare e terra, ovviamente. perchè negarsi qualcosa?
a Topogigio
mi spieghi meglio perchè infinito/reale=materia ?
alla galapagos esisteranno certamente specie di tartarughe marine, ma la “testuggine della galapagos” è di terra, è enorme e campa 150/200 anni, forse di più.
nome scientifico Geochelone nigra.
si può controllare qui:
http://it.wikipedia.org/wiki/Geochelone_nigra
e in moltissimi altri luoghi der webbe.
la distanza di un segmento finito non diventerà infinita, ma il senso dell’inifinita suddivisione riguarda l’analisi del moto, che ner paradosso di zenone e anche nel mio, sarebbe una serie infinita di qui/adesso, qui/adesso, qui/adesso…
insomma è l’impercorribilità della materia.
a meno di non ammettere che l’infinito si possa saltare.
metti.
oppure che l’infita suddivisibilità sia matematicamente giusta, ma una cazzata nella realtà…
non so, noi di roma ce la tiriamo da stupidi.
suddivisibilità?
cara Alcor, mi fa piacere che alle due e mezza di notte ti occupi di tartarughe; come ulteriore conferma di quel che dicevo ti segnalo quest’altro sito dove, al punto 2.2 si spiega come anzi il nome stesso Galàpagos derivi dal nome in spagnolo della testuggine marina. Fortunatamente il luogo non era infestato, ai tempi, da guerrieri greci più o meno arroganti…..
vedo ora i tuoi commenti, tash: io direi che suddivisibilità va bene, che dici?
La cosa che più condivido di quel che dici è “che l’infita suddivisibilità sia matematicamente giusta, ma una cazzata nella realtà”, (che sarebbe poi infinita), certo che la possibilità concreta di una infinita suddivisione è zero, ma tutto risale alla scelta dell’uomo di ritenere che in un segmento qualsiasi di retta ci siano infiniti punti.
Se, per dire, dicessimo che in un segmento di dieci centimetri ci sono dieci trilioni di trilioni di punti, agli effetti pratici tutto sarebbe uguale, nessuno, ma proprio nessuno, pensabile strumento di misura potrebbe smentire ciò. E il paradosso di Achille e della cheli non vi sarebbe. Ma sarebbe scomodo dal punto di vista calcolativo: per questo i fisici, in combutta con i matematici, hanno deciso per i numeri reali.
Pur essendomi chiarissimo il concetto della infinità divisibilità di un intervallo finito (e forse lo era anche a Zenone), credo che questo non risolva completamente il paradosso, o almeno credo sia giusto chiedersi perché il concetto di sommabilità di una serie, noto tutto sommato da più di 200 anni, non sistemi la questione, per molti.
Ripenso al pezzo citato di Borges che considera l’esposizione à la sparz semplicemente una corretta riproposizione del paradosso, non il suo scioglimento; il passo chiave è quando dice “la sua eternità [sua di Achille] non vedrà lo scadere di dodici secondi” e poi più avanti “non dimentichiamo di testimoniare che i corridori decrescono”.
Questo significa che il paradosso si apprezza a pieni dal punto di vista di Achille.
Da questo punto di vista si può riformulare, nei termini più precisi a cui giustamente invita Sparz, in questo modo: in che senso una successione infinita convergente raggiunge il proprio limite? Perché il limite non è parte della successione, non vi appartiene, come insieme. E’ dunque, questo “irrisolto” aspetto del paradosso di Zenone, una riproposizione in altra veste della (infinita?) contrapposizione fra infinito attuale e infinito potenziale. L’ostacolo che ogni matematico professionista che abbia cercato di convincere un dilettante che 0,999… è uguale a 1 conosce bene. Disputa dalla storia millenaria e che mi guardo bene dall’approfondire.
In questo senso se il paradosso di Zenone ha ancora qualcosa da dirci è che gli spaventosi abissi dell’infinito non hanno bisogno di numeri infinitamente grandi per essere enunciati, ma si intrufolano ovunque nel nostro modello del reale. E’ questo che fa concludere a Borges: “Zenone è incontestabile, a meno che non confessiamo la natura ideale dello spazio e del tempo”.
Perché non potrebbe darsi
che volessimo produrre una contraddizione?
Che dicessimo – con l’orgoglio di chi ha fatto una scoperta matematica:
“Guarda in questo modo produciamo una contraddizione”?
Ludwig Wittgenstein.
Vorrei ritornare al “gioco”, al “giocare” che proposto nella prima parte del post di Sparzani: la suddivisione dei pensatori in “legatori di paradossi” e “scioglitori di paradossi” [suddivisione infelicemente estesa, in campo letterario, a “manieristi” e “classici” che ha provocato, purtroppo, una diatriba O.T., rispetto all’argomento del post].
Quindi vorrei ripartire da tre affermazioni fatte, due di commentatori e una del postante, per tentare di capirne di più:
Dice liviobo: “risolvere matematicamente o logicamente il paradosso, è solo spostarlo in un’altra area percettiva”
Dice tashtego: “zenone trova una frattura tra il mondo e la sua concepibilità…”
Dice sparz: “il paradosso è sparito, il paradosso era originato da una assai peculiare maniera di dividere il tempo (finito) del raggiungimento in infiniti intervallini […]”
Ora.
Ammettiamo – cercando, ma col limite della mia capacità, poche, di usare un linguaggio se non preciso, impossibile per me, almeno comprensibile – che il paradosso sia stata una di quelle verità di cui un sistema formale (matematica) non era in grado di dimostrare né la verità né la verità della sua negazione, ma che questa situazione sia cambiata con la costruzione del calcolo infinitesimale e con la formulazione [non ne conosco la definizione esatta] della teoria del limite di Weierstrass.
Soltanto il sistema formale integrato (matematica attuale) risolve il paradosso?
E chiedo: la costruzione di tali strumenti risolutivi è stata resa possibile dalla assunzione di [quali non so] nuovi assiomi?
*
Quando il matematico formula i postulati di una teoria e propone un sistema assiomatico viene a collocarsi esattamente in quel punto in cui la *libertà* dell’invenzione (gli assiomi non sono né giudizi sintetici a priori né fatti sperimentali) si concilia con il carattere di rigorosa necessità della catena di successive deduzioni.[…]
appare allora come il segno di un possibile raccordo tra il fenomenico e il soggettivo, tra il determinismo del mondo e l’autonomia dello spirito come prerogativa del regno morale.”
[E questo potrebbe avere a che vedere con la via indicata da Topo Gigio: l’Amore]
PAOLO ZELLINI, Breve storia dell’infinito, Adelphi 1985, pag.131.
*
E quindi, l’accettazione del nuovo sistema capace di sciogliere il paradosso non comporta il fatto che si debbano accettare “nuovi assiomi”, che, se di assiomi si tratta, presuppongono una scelta?
E che questa scelta abbia come “prova” della propria legittimità soltanto il fatto che “funziona”?
E che questo suo funzionare sia anche funzionare nello scioglimento del paradosso di Zenone?
Cioè ad hoc.
Che di fatto può essere che lo “scioglimento” del paradosso dipenda dall’ accettazione di un “paradigma”, quello attuale, che mentre scioglie Zenone si lega con Cantor e Zermelo?
Ma che le cose sarebbero potute andare diversamente.
Oppure che la soluzione proposta non abbia alcun valore in altri ambiti, per esempio in filosofia?
*
“La dimostrazione di Zenone sembra tuttavia invulnerabile, nella sua *intenzione* ancor più che nel suo specifico svolgimento dialettico, da ogni confutazione che faccia uso del limite. Essa introduce un metodo generale di riduzione all’assurdo che fu ripreso anche da chi si preoccupò di neutralizzarne l’efficacia. Non senza ironia, c’è da supporre, Borges rammenta che fu proprio Aristotele a smontare con sdegnosa brevità gli argomenti di Zenone, ma per usarne poi il paradigma allo scopo di confutare Platone. Una volta entrati nella sfera dell’enigma è difficile sottrarsi all’impressione che ogni argomento dotato di apparente consistenza si rovesci in errore.”
PAOLO ZELLINI, Breve storia dell’infinito, Adelphi 1985, pag.41
*
Ecco quello CHE MI PIACE PENSARE è che “qualunque soluzione” venga data al paradosso è frutto di una “scelta alla soluzione”, ma è altrettanto “gratuita” della scelta opposta di considerarlo ancora vivo, anche perché, chi ne dimostra la fine, usa gli stessi strumenti formali usati nel paradosso per supplire a debolezze in altre parti del sistema.
quella voce di encarta è sbagliata, sparz.
le tartarughe giganti per cui sono famose le gala-pagos e da cui prendono il nome, sono terrestri: Geochelone nigra.
come preferisci @ sparz, non ho mai cercato di convincere nessuno
“Fortunatamente il luogo non era infestato, ai tempi, da guerrieri greci più o meno arroganti…..”
interessante chiusura del commento, ambigua, ci penserò…
cmq chi vuole togliersi la curiosità può andare qui
http://spot.colorado.edu/~humphrey/fact%20sheets/tortoise_galapagos/tortoise.htm
e vedrà i suoi grandi unghioni, fatti per il terreno, mentre la tartaruga marina al posto degli unghioni ha quelle belle spatole che si vedono qui sopra nella foto del post
zenone mi folgorò al liceo.
e tale sono rimasto (folgorato) per tutti questi anni.
e c.s.n.f., direte voi.
@sparzani …
sto per dare il via a una specie di delirio… ma fa lo stesso: consideriamo, per un attimo, spazio e tempo come due strumenti attraverso cui la realtà diventa misurabile in termini di denaro… quanto hai lavorato? ecco la paga! quanto costa questo orto? ci stanno dentro duecento piante di pomodoro che in tre mesi possono produrre tremila pomodori… vedi tu … e così via; consideriamo adesso Zenone, e cioè leggiamo fra le sue parole, se ci va bene e si stiamo alla provocazione, un paradosso che mette in discussione, sul piano logico, la velocità proverbiale di Achille per dirci che possiamo mettere in discussione l’idea della misurabilità (economica) della realtà… e cioè che nel rapporto con l’infinito il contadino greco è costretto ad uscire dalla sua condizione di “dulcis in fundo” (che significa “persona affabile in un campo”), o di “idiota” (“uomo privato”, considerato come singolo proprietario) che si trova di fronte al venditore/geometra/misuratore spazio-temporale e, alzati gli occhi all’orizzonte stabilisce che ragionerà con un’altra logica.
ps. i pezzi sono fantastici
@l’ignorante. Spero non ti dispiaccia se provo a rispondere io ad alcune delle tue domande, dal mio punto di vista. Se il problema di Zenone è un problema di “raggiungimento del limite” c’è, effettivamente, un preciso assioma sottosante. Ma nonostante la sua comprensione sia moderna, la sua formalizzazione è antica. E’ l’assioma di Archimede, fondamentale nell’approccio assiomatico all’aritmetica che fece Dedekind nell’800.
La sua formulazione è assolutamente semplice: ogni numero, per quanto piccolo, sommato con se stesso un numero sufficiente di volte diventa arbitrariamente grande (si può costruire una montagna con granelli di sabbia, come viene divulgato a volte).
Negarlo dà spazio ad una matematica molto interessante; è la cosiddetta “analisi non standard”, formalizzazione del 1960 della vecchia teoria degli infinitesimi che tanto faceva arrabbiare il vescovo Berkeley nel ‘700 (celebre la sua definizione di infinitesimi come “spettri di quantità morte”). Sulla retta non standard Achille avrebbe i suoi problemi a raggiugere davvero la tartaruga. Agli inizi del ‘900 ha provato un geometra italiano, Veronese, a studiare la geometria di rette e piani non archimedei. Sembravano emerite seghe mentali fino a quando
questi studi non hanno rifatto capolino all’interno della teoria dei codici, quella che sottende la crittazione e decrittazione dei segnali digitali.
Questa assioma è, a suo modo, l’unico assioma non completamente autoevidente della aritmetica assiomatica (un po’ come l’assioma delle parallele per la geometria non euclidea). Tant’è che ne son state date versioni alternative (l’assioma di Tarski: 1+1>1, ma se uno non sa di queste cose corre il rischio di sembrare una stupidaggine). Mi fermo qui per non essere importuno.
Va bene. Però Olshcky nel 1902 rovescia la questione degli insiemi trasn-finiti (suo l’aforisma: Dio non gioca a biglie, le crea) nella nota equazione multi-derivativa, da cui discendono tutta una serie di conseguenze delle quali Zenone, ovviamente, non poteva essere a conoscenza.
Vi si presuppone che lo spazio e il tempo siano, più che infinitamente suddivisibili, super-comprimibili in ultra frazioni di Kères. Le conseguenze sulla topologia sono note: un guanto sinistro rovesciato dà un guanto destro, diceva Kères, ma provate a rovesciare una scarpa destra: non senza applicare un certo sforzo, otterrete infiniti mondi tutti egualmente probabili, alcuni dei quali non comprimibili. È esattamente in uno di questi mondi che siamo capitati, avrebbe detto Zenone, ma si sbagliava. Dopo aver infinitamente suddiviso lo spazio tempo, occorre comprimerlo, come fa Achille con i piedi, non differentemente da come fa uno shuttle con i suoi booster. Solo così si potrà raggiungere la tartaruga, forzando lo spazio tempo e non, come magari si vorrebbe, mettendosi a dormire. «Achille non era il solito loser, come la maggior parte di noi», scrive Vincent Trotini nella sua prefazione all’edizione di Princeton del 1938 dei Principia, «come che sia, per raggiungere la tartaruga occorre spendere una quantità di energia diversa da zero: lì sta il punto». E direi che è vero: la questione risiede, secondo un profano come me, nel concetto di diverso-da-zero: piccolo, ma diverso da zero, infinitamente. Se poi qualcuno può portare qui le prove di aver incontrato, almeno una volta nella vita, qualcosa uguale a zero, sarò il primo a ri-credermi.
Ovviamente.
:D (per un momento mi son chiesto se le ultrafrazioni…naaahhh)
@ Da
La mia ulteriore intuizione è questa:
Infinito = Materia + Resto
Come dicevo, l’eccedenza è il resto. Come è ovvio, l’infinito meno il resto è uguale alla materia. Per astrazione, faccio questo ragionamento: l’infinito genera la materia, ma in questa operazione si forma una eccedenza, e questa eccedenza è il resto. Quindi molto semplicemente se abbiamo un infinito e lo “mettiamo” nella materia (materia quoziente) dobbiamo avere una eccedenza (resto).
Questo per contraddire coloro che credono alla materia come fabbrica di pensiero.
quindi l’eccedenza sarebbe il pensiero, se ti ho capito bene. Tesi non nuova, per esempio la depense di Bataille ecc , anche se magari tu la intendi in modo completamente diverso.
Interessante, anche se per me non governabile. Ma in ogni caso leghi infinitezza e materia, poi vai a sapere la cosa che contiene l’altro qual’è, o viceversa. l’uno nell’uno è sempre im/possibile.
bella la metafisica che schizza fuori appena può dalla mente liceale dell’intellettuale: ogni scusa è buona per buttare il cervello oltre l’ostacolo (logico/matematico) e ricominciare a blaterare le solite vecchie care cazzate…
a snaporaz
La logica comprende, o meglio: sarebbe ora che vi si avvicinasse, anche lo slancio di guardare oltre, non certo quel raziocinio a cui ti appelli.
guardiamo oltre, si capisce.
così si fa a meno del riprovevole dato fisico matematico.
che non garantisce VERITA’, d’accordo, ma che almeno fa parte di un processo collettivo e comunicabile di conoscenza.
poi fate voi, andate oltre.
voi chi? ogni cosa si avvita su di sè, se presa in maniera univoca, anche la matematica, la fisica,la metafisica, la tecnica (tutte cose a cui guardo con molto stupore più che appartenenza, niente affatto riprorevoli). il problema non è affatto una comoda verità, è che ci sono parole chiave che subito attraggono, altre che provocano immediata ripulsa, su questo c’è molta fatica da fare
@
No, l’eccedenza non è il pensiero. L’eccedenza è l’amore, come avevo scritto in precedenza. Dunque una somma infinita che si fa rientrare in un quoziente di materia produce (scrivo “pruduce” perché non so cosa altro scrivere, al momento) un resto; questo è verificabile per esempio con la semplice formula: n(n + 1)/2.
Ps: non sono sicuro si debba scrivere che una somma infinita si fa rientrare, dato che come sopra ho detto ciò dà un resto di eccedenza, per il cui ragionamento l’infinito è diviso per la materia quoziente; ad ogni modo la formula matematica e quella intuitiva non si contraddicono.
è un ragionamento che dà le vertigini, come guardare in un telescopio. grazie, per il momento
giusto per ridare qualche significato ad alcuni termini che provengono dalla matematica. Intanto la formula citata n(n + 1)/2 serve unicamente ad ottenere la somma dei primi n numeri naturali, esempio: 1+2+3+4+5= 5(5+1)/2 = 15. Le “somme che contengono infiniti addendi”, di per sè non hanno senso, cioè dobbiamo, se lo riteniamo opportuno e utile, dargliene uno noi, visto che non è in linea di principio possibile eseguire infinite somme. Queste infinite somme in matematica si chiamano serie e si riesce a dare un senso alla loro esistenza mediante il concetto di limite. In questo modo si ottiene ad esempio che la serie ½ + ¼ + ⅛ + ecc. citata nel testo esiste ed è uguale a 1. Invece la serie 1/2 + 1/3 + 1/4 + 1/5 + ecc., che pure gode della proprietà che i suoi termini “vanno diminuendo” non esiste, il ché in questo caso vuol dire che succede che, pur di sommare abbastanza addendi, si supera qualsiasi numero finito. Si può anche descrivere questa situazione dicendo che “la somma è infinita”, ma il senso di queste parole altro non è che appunto “pur di sommare….”.
per rispondere all’ignorante, e a sparz se includeva anche le mie fra le parole con un senso impreciso, ma senza addentrarmi troppo nella questione ammirevolmente ma troppo tecnicamente posta da chik67, che peraltro para a conclusioni simili alle mie, esemplifico molto in breve e nello spirito della chiacchierata cosa intendevo dicendo che achille effettivamente non raggiunge la tartaruga: di fatto noi non sappiamo mai cosa avviene “dall’altra parte” di noi, quel che possiamo dire è che una macchia a forma di achille ne raggiunge una a forma di tartaruga, se achille era in rosso ad es. una chiazza rossa, proiettata nei nostri neuroni dalla retina, ne sopravanza una verde, ipotizzata con lo stesso sistema. e lo stesso accade per qualunque sistema scitnifico di verifica. questa contraddizione, questa insolubilità del rapporto fra noi e l’esterno è obiettiva – ne sapevano qualcosa wittgenstein o merleau ponty – e su questa insolubilità obiettiva gioca il paradosso.
@ Da
Prego.
@ll
La mia era un’idea su cui mi ero soffermato qualche tempo fa ripassando un libro di matematica, e vedendo questo articolo mi era venuta in mente, quindi ho voluto provare a proporla. Dunque, se sia stato utile o meno, non so, però mi è piaciuto. Grazie per la discussione.
“So bene che si potrebbe dire: “Siamo ignoranti e tuttavia dobbiamo agire. Per agire, non abbiamo il tempo di dedicarci a un’indagine sufficiente a dissipare la nostra ignoranza; d’altronde un’indagine del genere richiederebbe un tempo infinito. Dobbiamo, dunque, deciderci senza sapere; dobbiamo farlo confidando un po’ nella buona sorte e dobbiamo seguire delle regole senza credervi troppo. Ciò che so non è se la tal cosa sia vera, ma se per me sia meglio agire come se lo fosse”.
JULES-HENRI POINCARÉ, La scienza e l’ipotesi, Bompiani 2003, pag. 277.
*
Mi viene da proseguire il vecchio gioco. E dopo gli scioglitori/legatori di paradossi, i manieristi/classici letterari, proporre quest’altro: “descrittori della giusta realtà”, ai quali, però, implicando ogni descrizione della realtà un linguaggio, si contrappongono i “verificatori di linguaggi”.
Dove si situa oggettivamente il paradosso di Achille e la Tartaruga?. In molti si sono posti il problema in questo thread.
Quale tipo di problema è?
Perché se fosse un problema empirico, come è stato detto, sarebbe un’idiozia. Non c’è alcuno dubbio che Achille raggiungerà la tartaruga.
Oppure è un problema di “dimostrazione”?
Anche questo è stato detto, e la dimostrazione è stata data.
E se non fosse stato tutto questo, ma essenzialmente un “problema scettico”?
Nel senso di affermazione di una pretesa: che, nel caso nascessero “dimostrazioni” della sua non.validità, queste verrebbero inficiate, “comunque”, da qualcos’altro?
La cosa è stata accennata in vari modi, ma l’indicazione risolutiva mi pare quella di Liviobo 20.03, 16:37:
“per farla breve cito un paradosso di wittgenstein: come possiamo affermare che 2+2=4? se un diavoletto, mentre eseguiamo l’operazione, aggiunge un’unità, non fa forse 5?”
Insomma, chiedo, dal momento che il paradosso di Zenone è stato dimostrato non essere paradosso – in base a costruzioni matematiche non ancora esistenti al momento della sua formulazione – non è che, dopo questo, sia venuto fuori qualcosa capace di dimostrare che quella “dimostrazione” non può essere considerata una “dimostrazione?
*
“L’induzione applicata alle scienze fisiche è sempre incerta giacché poggia sulla credenza a un ordine generale dell’Universo, un ordine che è fuori di noi. L’induzione matematica, ossia la dimostrazione per ricorrenza, invece, si impone necessariamente, poiché non è che l’affermazione di una proprietà della mente stessa.”
JULES-HENRY POINCARÉ, op. cit., pag. 31.
*
Perché è questa la domanda : il paradosso di Zenone riguarda le scienze fisiche? In questo caso nessuno avrebbe da obiettare sia al fatto che Achille raggiunga la tartaruga , sia al fatto che tutto ciò è dimostrabile. Una volta escluso il dubbio che l’induzione possa far parte di una “vera” dimostrazione.
Oppure riguarda la matematica, la filosofia della matematica o la filosofia della mente?
Perché in questo caso non c’è dimostrazione che tenga.
Tashtego: “una frattura tra il mondo e la sua concepibilità.”
Infatti, in quest’ultimo caso, quando non c’è alcun Universo a garantire la permanenza delle condizioni date, il sistema di calcolo delle previsioni – cosa succederà nella corsa di Achille e la tartaruga ? – dipende dall’applicazione di regole e dall’applicazione delle regole per applicare le regole.
Un terreno in cui è possibile rifarsi, scetticamente, a un altro paradosso, chiamato “Kripgenstein”, che, assieme al “blerde e vlu” di Goodman, da quattro decenni – come Zenone da due millenni – disturba il sonno dei pensatori che vi si misurano.
Non starò a spiegare – se mai ne fossi capace –, nei prticolari, tutta la faccenda.
Wittgenstein prende inizio dal “linguaggio privato”. Ecco le due proposizioni fondamentali che illustrano il suo “problema scettico”, nelle “Ricerche filosofiche”:
201. “Il nostro paradosso era questo: una regola non può determinare alcun modo d’agire, poiché qualsiasi modo d’agire può essere messo d’accordo con la regola .”[…]
202. […]“E perciò non si può seguire una regola ‘privatim’: altrimenti credere di seguire la regola sarebbe la stessa cosa che seguire la regola.”
Tutto l’altro lavoro, fatto per farci capire, è in: “SAUL KRIPKE, Wittgenstein. Su regole e linguaggio privato, Boringhieri 1984.
Domanda finale: poiché Kripgenstein “dimostra” che, per noi, se lui ce lo chiedesse, la somma 68+57, non fa 125, ma, naturalmente, 5, come abbiamo sempre pensato, e che noi non possiamo confutarlo perché non esiste alcun “fatto” che dimostri diversamente (nemmeno Dio potrebbe scoprirlo), possiamo usare lo stesso Kripgenstein per “dimostrare” che “la somma di infiniti numeri *non* può dare un numero finito” o che “la serie 1/2 + 1/4 + 1/8 ecc. *non* è uguale a 1”?
@ l’ignorante
Scrive: “Insomma, chiedo, dal momento che il paradosso di Zenone è stato dimostrato non essere paradosso – in base a costruzioni matematiche non ancora esistenti al momento della sua formulazione – non è che, dopo questo, sia venuto fuori qualcosa capace di dimostrare che quella “dimostrazione” non può essere considerata una “dimostrazione?”
Dico che è così. Il paradosso di Zenone è un vero paradosso. Posso domostrare quanto dico, e soprattutto che non lo dico per gioco, benché mi abbia fatto piacere esporre la mia idea. Mi occorre però un po’ di tempo e un articolo su NI.
sono in trepida attesa caro Buenasorte, cosa vuol dire “un articolo su NI”?
@l’ignorante (che tanto ignorante non pare); se prendiamo l’argomento del linguaggio privato di Wittgenstein, cade ovviamente qualsiasi possibilità di dimostrare alcunché. Tuttavia W. stesso superò il proprio argomentare con la presa in carico del contesto. Vedi Kripke.
a proposito di vaghezza, dov’è che wittgenstein “prese in carico” questo contesto? e comunque dov’è la bolla?
Zenone sconfitto da Weierstrass mi fa venire in mente questa scena:
http://www.youtube.com/watch?v=LN5dN9y4xCE
@liviobo no, io non ne facevo un problema di conoscibilità del reale, senza la quale stiamo a pettinare bambole, nè un problema di rapporto tra modello e realtà. Nella realtà Achille sorpassa, non c’è ambiguità di previsione; dunque il modello è giusto se prevede il sorpasso, sbagliato altrimenti.
Sparz dice che il modello è giusto perchè le serie si sommano. A me pare, in parte, una risposta col trucco. Le serie si sapevano sommare già nel Seicento. E’ infatti di quegli anni la prima “proposta” di scioglimento del paradosso tramite serie. Però restava un problema: in che senso la serie raggiungeva la sua somma dopo infiniti passi? Non è un problema che mi invento io. Era il problema della buona definizione di limite.
Un problema più carogna del previsto; è vero che lo risolve Weierstrass, (dopo 200 anni) ma lo risolve con un buco. La sua definizione di limite ha bisogno dei numeri irrazionali. E cosa sono i numeri irrazionali? Il limite di successioni di numeri razionali. Un ragionamento un po’ circolare non trovi? Bisogna riuscire a definire i numeri irrazionali senza usare i limiti.
Questo lo fa Dedekind alla fine del’800. Ma ad un prezzo. L’infinito attuale. Per Dedekind un numero E’ un insieme infinito. Puf’ il paradosso di Zenone scompare, perché una serie convergente è la sua somma (ci vogliono altri 80 anni per sistemare Dedekind).
Ma non l’horror vacui che suscita, per colpa sua adesso l’infinito ce lo portiamo in tasca tutto intero.
Non riesco a seguirvi, ma lo stesso mi pongo la classica domanda del filosofo ingenuo.
Manco di cultura matematica, forse di cultura tout court, ma da quel poco che ne ho esperito intravedo nella matematica una sorta di irriducibilità alla materia, o, se si vuole un’irriducibilità della materia alla matematica.
Se ti serve lo zero e ti serve infinito, se ti servono le frazioni, le radici quadrate, eccetera, beh, sappi che prima o poi troverai un punto, un luogo del rapporto materia/mente in cui il sistema tramite il quale puoi costruire aerei e ponti e altra roba utile, mostra un lato perverso, sinistro.
Dentro quegli aerei, quei ponti, si annida l’irrazionale, l’approssimazione, l’astrazione, l’indeterminazione, si annidano le non congruenze tra il linguaggio matematico e il suo referente, si acquatta il problema della precisione, della misura, l’irraggiungibilità della perfetta esattezza, in definitiva la riottosità dell’esistente a lasciarsi rappresentare in toto dalla matematica e, ancora di più, a lasciarsi mano-mettere dalla tecnologia.
E sto parlando di matematica.
Con la fisica le cose diventano ancora più misteriose.
A questo punto, se esistesse, il Motore Immobile potrebbe esprimersi in questo modo, ammonendoci: come è possibile che un primate che si è dotato (misteriosamente evolvendolo) di un centro cerebrale capace di rappresentarsi il mondo in modo da dargli notevoli chance di sopravvivenza, metti nella savana d’Africa di centocinquantamila anni fa, pretenda con quello stesso strumento di «capire» (dal lat. capere, «prendere») Universo e Materia senza che gli sfugga, eternamente, qualcosa?
Concordo con questa osservazione. Ma d’altra parte sta l’efficacia
del linguaggio matematico nel descrivere seppur parzialmente universo
e materia.
Non a caso Wigner ha parlato di “irragionevole efficacia della matematica
nelle scienze naturali” concludendo (in un trionfo di retorica, perlatro)
“The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it and hope that it will remain valid in future research and that it will extend, for better or for worse, to our pleasure, even though perhaps also to our bafflement, to wide branches of learning”
Sono perfettamente d’accordo con Tash.
Il problema, a questo punto, per me, si pone in questo modo:
come si fa a parlare, si può parlare di quello che sfugge alla misura, alla scienza?
Ben sapendo che la scienza è una sorta di opera impossibile di bonifica di una palude infinita, e che può costruire soltanto punti leggermente più avanzati di osservazione, è lecito domandarsi: quale altro tipo di storie possiamo imbastire sull’Universo?
Dobbiamo basarci sui dati materiali che provengono dalla nostra conoscenza, accumulata mentre percorrevamo il sentiero che ci ha portato al punto più avanzato di osservazione, oppure, tenendo conto che quel piccolo sentiero poco ha a che fare con l’abisso infinito che ci sta davanti, ammettere che ci possano essere “altri” modi raccontare, “altri” modi di vedere?
In effetti, qui sta la funzione dello “scettico”: è quello che dice: “non state a riposarvi, buttatevi!”.
Solo lo scettico può riaprire lo scenario oltre il “Su ciò, di cui non si può parlare, si deve tacere”, se si pensa che il misticismo non sia una forma di conoscenza assoluta, ma soltanto una forma di appercezione del proprio sé individuale.
L’unione tra scetticismo e misticismo, Scholem la chiama “misticismo nichilista”: il “guardiano della porta” che vigila affinché questa rimanga sempre aperta. Il suo nemico è il linguaggio.
“Dentro quegli aerei, quei ponti, si annida l’irrazionale, l’approssimazione, l’astrazione, l’indeterminazione” (Tashtego).
Mi è venuto in mente, ora, a leggere questa frase di Tash, l’episodio che portò alla rottura definitiva tra Wittgenstein e Turing.
Turing frequentava le lezioni di Wittgenstein e le loro liti avvenivano per lo più sul tema della “contraddizione”. Era il periodo più infuocato delle discussioni sulla “crisi dei fondamenti”.
Naturalmente Turing vedeva la contraddizione come opera del diavolo, mentre Wittgenstein insisteva a dire che la cosa non era determinante, giustificandola, teoreticamente, a modo suo.
L’atto finale avvenne quando Turing affermò che con una matematica contradditoria non si sarebbero mai potuti costruire “ponti stabili”.
Facile immaginarsi cosa sostenne Wittgenstein.
Non si videro più.
anch’io trovo assai bella la sintesi di tashtego. magari la radicalizzerei sostituendo a centro cerebrale, corpo.
@chik67
io non dico: achille non raggiunge la tartaruga, perchè tutto è inconoscibile. io dico: esiste un “determinato” livello della realtà, a cui achille non raggiunge la tartaruga, e a questo mi ha fatto accedere il paradosso. un paradosso è sempre una comunicazione di tipo metalinguistico, il cui fine è una conoscenza altra rispetto a quelle che pone in contraddizione. zenone non è un mikebongiorno che pone quiz ai posteri, altrimenti avrebbe prospettato lui stesso una soluzione. zenone semmai esemplifica una percezione, che è quella che la realtà è immobile. chi risponde al quiz, non dico che perde il tempo, ma si trastulla con complesse bazzecole. il problema di fondo invece è proprio il rapporto fra modello e realtà, che è appunto un problema di tipo metalinguistico, e dunque metafisico.
che cosa ha aggiunto godel al mondo, se non un “sentimento” nuovo del mondo? in cosa consiste, ultimamente e radicalmente, qualsivoglia teroria che riguardi i fondamenti, se non in un riassetto, in una permutazione, in una ricolorazione di chimismi del nostro corpo?
Mi chiedevo se qualcuno di voi ha avuto modo di vedere l’ultimo film di Takeshi Kitano. Il titolo è: Achille e La Tartaruga.
Io ne ho rintracciata una copia in giapponese con sottotitoli in spagnolo (che non parlo).
Ma non è che, se il problema di Zenone è empirico, e quindi da risolvere con la fisica, ancora meno c’è soluzione, annullandosi completamente il salvagente del “limite”?
Facciamo correre i Due, secondo la serie 1/2, 1/4, 1/8 ecc. di una qualche distanza iniziale. Questa serie porta a una diminuzione tendente allo zero della distanza compiuta in ogni frazione. La distanza sarà uguale a zero raggiunto al limite, quando Achille supererà la Tartaruga.
Ma ciò non potrà avvenire mai. Perché prima di raggiungere lo zero, verrà raggiunta la distanza rappresentata dalla costante di Planck, che per quanto piccola è maggiore di zero.
Non siamo più nella fisica classica, ma nella meccanica quantistica e secondo il “principio di indeterminatezza” di Pauli, a quelle dimensioni, è impossibile sapere cosa succede.
Soltanto un calcolo complessivo del comportamento di tutte particelle elementari che compongono i Due corpi ci potrà dire che PROBABILMENTE Achille raggiungerà la Tartaruga.
Ma soltanto se avrà superato [come?] l’Abisso del Nulla.
La cosa più affascinante in tutto questo sarebbe, in effetti, cercare di legare Wittgenstein, Gödel, Turing e Pauli in difesa di Zenone.
Cioè appurare, facendosene fieri, che esistono sì verità che possono essere dimostrate, ma che ce ne sono altre che mai potranno esserlo. E che tra questi sta Zenone.
Ho sempre considerato, infatti, il “teorema di incompletezza”, il vero paradosso dei nostri tempi.
E siccome lo stesso Gödel considerava il “problema della fermata” di Turing come la versione più aggiornata e rigorosa di quello, aggiuntovi il Pauli del “principio di indeterminatezza”, legarli al Wittgenstein delle “regole e linguaggio privato”, che, a pensarci almeno un po’, ara esattamente lo stesso terreno.
Questi tentativi avrebbero in effetti un obiettivo principale, che non è solo quello di partecipare agli infiniti giochi che con il paradosso si possono fare, ma cercare di dimostrare un’altra verità: che chi ha scritto la “favola” messa all’inizio della prima parte di questo post, Carlo Emilio Gadda, non solo è il più grande scrittore italiano del ‘900, ma anche una delle menti più acute che il nostro paese possa vantare:
“Particolarmente suggestivo, anche perché indicherebbe non una derivazione ma piuttosto un’anticipazione (a livello “intuitivo”, beninteso), è il confronto che si può istituire tra il principio gaddiano dell’”impossibile chiusura di un sistema” e, nella logica matematica, le teorie dell’”incompletabilità dell’aritmetica formale”.
Secondo il cosiddetto primo teorema di Gödel (formulato nel 1931 [mentre l’”intuizione di Gadda è del 1928, nota mia], in ogni sistema assiomatico c’è almeno un enunciato che non è deducibile nel sistema, ma soltanto all’interno di una sistema più ricco.
È questa l’”intima angoscia”, l’”indeterminatezza” di cui, secondo Gadda, soffre qualsiasi “sistema di relazioni espresso dalla conoscenza umana”:
perché
“ogni sforzo conoscitivo integratore della realtà
ha un punto maligno o punto difettoso
ove i nodi della costruzione
vengono al pettine della critica.”
GIAN CARLO ROSCIONI, intrroduzione a: Carlo Emilio Gadda, Meditazione milanese, Einaudi 1974.
Scusa liviobo non ho capito.
O il problema è della realtà, a qualunque livello tu ti ponga.
O il problema è del modello nel senso che:
a. dimostra una contraddizione intrinseca al modello oppure
b. il modello produce un risultato diverso dalla realtà.
Il problema della realtà non si pone, perchè nella realtà empirica chi va più veloce sorpassa, con buona pace di chi vorrebbe applicare la meccanica quantistica ai corpi macroscopici.
Allora è nel modello. Quello che Zenone porta è la comprensione del fatto che il modello ingenuo che abbiamo in mente non funziona. Per funzionare, cioè per produrre lo stesso risultato dell’osservazione empirica, deve essere estremamente più sofisticato di quanto non appaia a prima vista. Senza bisogno di scomodare Godel.
@chik67
@chick 67
io non ho pensato di “applicare la meccanica quantisca ai corpi macroscopici”, e mi spiace una reazione così violentemente negativa a una domanda che può anche essere ingenua:
sediamoci, come ha fatto Einstein, sulla più avanzata particella elementare della punta della calzatura di Achille, portando con noi uno strumento di osservazione, non importa quello che sia
applichiamo il nostro strumento di osservazione a ciò che può succedere in quella dimensione, uguale a quella della costante di Planck che ci separa dallo zero, dal “limite”, per registrare, empiricamente, cosa succede in quel punto, in quel momento:
non è che che vediamo alcun corpo macroscopico, ma, a quella dimensione, solo aggregazioni di particelle che rispondono alle leggi della meccanica quantistica?
Insomma se tra la costante di Planck e lo zero c’è una differenza, c’è anche qualcosa che necessariamente ignoriamo.
Achille, empiricamente, raggiunge la Tartaruga, ma qualsiasi informazione vogliamo raccogliere per un modello, ci è impossibile raccoglierla.
Il modello è incompleto, perchè non può integrare in sè ciò che succede in quell’intervallo.
Godel non c’entra col paradosso, c’entra col fatto che ci sia il paradosso.
sono piacevolmente sorpreso che questa conclusione del ciclo di Achille e la Tartaruga abbia suscitato un così ricco dibattito. Ogni tanto sarebbe bene ripartire con i piedi bene attaccati a terra; ovvero: capisco che Wittgenstein e Gödel siano autori ancora molto popolari, data l’apparente stranezza di alcuni loro risultati, però mi pare anche importante non adoperare cannoni per ammazzare le mosche.
Io credo davvero che lo scopo di Zenone nell’enunciare il suo paradosso — per quel che se ne sa, perché ripeto che della sua opera autentica abbiamo solo frammenti citati da altri — sia stato non certo quello di dimostrare che Achille non raggiunge la tartaruga, quanto piuttosto quello di mettere ben in guardia dai pericoli del non accurato ragionare. Dai pericoli cioè derivanti dal tirare conclusioni a partire da premesse senza che sia rispettata una regola chiara per questo “tirare”. Ovvero dai pericoli del linguaggio non abbastanza attentamente formalizzato.
I problemi di Gödel sono del tutto diversi; i suoi sono autentici teoremi, che potranno — alcuni — sembrare stupefacenti e strani, ma che sono incontrovertibilmente dimostrati.
L’allusione poi alla meccanica quantistica mi è molto piaciuta; non scherzo, mai mi sarebbe venuto in mente di connettere la faccenda dei trattini di spazio sempre più piccoli con la lunghezza di Planck, e, si potrebbe analogamente aggiungere, di connettere gli intervalli di tempo sempre più piccoli con il tempo di Planck. Un colpo da maestro. Va detto allora che, dal punto di vista della meccanica quantistica, dopo il famoso tempo a/(V-v), la probabilità di trovare — facendo un’osservazione del sistema — Achille al di là della tartaruga è molto alta, cioè è pari a zero virgola un numero di nove molto alto, ma non è 1. Ma qui si entra davvero in un campo nel quale la libidine dell’applicazione di una qualche teoria fisica alla realtà ha toccato il fondo.
@l’ignorante sappiamo tutti benissimo che le discussioni in rete hanno i loro rischi; ti assicuro che la mia reazione non voleva essere “violentemente negativa”, ironica più che sarcastica, non sentirti offeso, non era il mio intento.
Volevo solo dire, senza farla lunga, che se cercassimo di ricostruire un qualunque evento macroscopico come somma degli eventi quantistici dei singoli atomi che compongono il sistema, cosa che in linea di principio potrebbe pure essere possibile, altro che Zenoni e tartarughe. Di problemi ne incontreremmo tantissimi. Il cosiddetto “limite semiclassico” è ancora lungi dall’esser capito fino in fondo. La matematica pertinente è ancora in pieno e tumultuoso sviluppo e non tutti i risultati raggiunti negli ultimi vent’anni sono stati ancora pienamente digeriti. Insomma, un ginepraio.
Senza infognarcisi è sufficiente rilevare che il modello coi numeri reali è ben adatto alla meccanica classica, macroscopica, dove lo spazio ed il tempo possono ragionevolmente essere ritenuti continui ma non a quella quantistica che ragiona sul discreto. Nel fatto che non esista un modello unico che valga a scala macroscopica o microscopica, però, non c’è un paradosso interno alla matematica, per questo lascerei il povero Godel a riposare in pace.
Mi scusi Sparz
volevo sviluppare questa idea in un articolo.
Ecco l’idea:
b(h+1)/2
dove b è la base di un triangolo rettangolo; h è l’altezza; e dove b=h, cioè il triangolo ha i cateti uguali.
L’altra formula, quella delle serie, è:
n(n+1)/2
Ecco qui. Io ci trovo una corrispondenza, anzi, sono proprio la stessa espressione.
A questo punto – ecco la trovata – scrivo l’area del triangolo:
b(h)/2
e accosto a questa formula quella delle serie, oppurtunamente combiati gli n con base e altezza di un triangolo.
Ecco, questa è l’eccedenza di cui parlavo.
Immaginiamo di costruire una piramide con blocchi quadrati di un metro per lato. Mettiamo dieci blocchi alla base, poi nove, poi otto, e via così fino alla sommità, in cui mettiamo un blocco. Il totale dei blocchi della piramide risulta essere 55, vale a dire 10(10+1)/2.
In pratica, ho preso la misura della base, dieci blocchi; l’ho moltiplicata per l’altezza, dieci, ho aggiunto metà della base, o dell’altezza, e l’ho divisa per due. L’eccedenza è rappresentata dalla metà della base o dell’altezza; ed è una eccedenza rispetto al disegno di un triangolo, cioè l’eccedenza tra l’area di un triangolo disegnato e l’area di un triangolo, per esempio una piramide, costruito con blocchi di misura di lato 1.
Lo so, sembra una cosa che non c’entra col paradosso, eppure proprio con questo esempio volevo spiegare che una misura non reale, come l’area di un triangolo perfetto, cioè immaginario, quando viene portata nel concreto, cioè costruita per esempio con blocchi di lato uno, di lati uguali, produce una eccedenza. Per questo il paradosso è valido. Credo.
@chick67
ho l’impressione che il senso profondo (fenomenologico? mistico?) del mio riferimento a godel (quale puro esempio) non sia stato ben compreso. forse dovrei partire da paradossi ancora più esplicitamente legati alla percezione, come quello dll’anatra-coniglio, e dalla loro indecidibilità, che è molto poco legata a quella di pauli o heinsenberg. ma ora sono in partenza, spero di trovare occasione…
Niente sapevo del “limite semiclassico”.
Vista l’indicazione, interessantissima, di chick67 sono andato a cercarlo nel web.
Dio santo! mi sono perso in foreste di alberi mostruosi abitate da animali favolosi.
Sono però riuscito a scovare un sito quasi alla mia portata:
http://www.gardaline.it/la-pentola-guardata-non-bolle-mai-2706.html.
Potrebbe un esperto dare un giudizio su questa esposizione dell'”effetto Zenone” in meccanica quantistica, detto anche “la pentola guardata non bolle mai”?
Magari in forma essenzialmente “letteraria”.
A me pare che ne valga la pena, per rivitalizzare almeno un po’ le fantasie di certi scrittori – o pseudo.tali come me – sommersi da quella collassata della NIE.
Insomma: una volta definita la serie 1/2,1/4,1/8 ecc., per qualsiasi misura iniziale, avvicinandosi le zero, l’intervallo, che per Achille e la tartaruga erano passi, nel caso della “pentola guardata non bolle mai” sarebbero le “osservazioni”, le “misurazioni”: le radiazioni che investono la particella.achille che, attraversando un ultimo tratto, deve “superare” la particella.tartaruga.
Ora, a quanto ho capito io, qua non si tratta affatto di “superamento” e non si tratta affatto di confronto tra due particelle, ma tra due stati di una stessa particella.
Piuttosto che di Achille e la tartaruga, come dice “il postante della pentola”, si tratta della “freccia” di Zenone.
Negazione del movimento tout court per la freccia, impedimento di ogni “decadimento” delle particelle sotto certe condizioni di osservazione.
Ecco, vorrei sapere, dal momento che “il postante della pentola” nega che la casualità delle interazioni in una camera a bolle possano determinare l'”effetto Zenone”, a quale intensità di misurazioni, nel tempo, si deve arrivare perché questo manifest
*
Viene fatta, in quel post, una obiezione a Wigner – per altro già “richiamato” da chik67 in questo post – per quanto riguarda l’ipotesi che la lunghezza d’onda di una particella collassi qquando l’informazione raggiunge la coscienza dell’osservatore.
Chiarire, per quanto è possibile, questo punto sarebbe interessante.
Ricordo infatti che una discussione che può avvicinarsi a questi temi – contribuendo a chiarire l’ambiguità che sembra esserci tra “misurazione” “osservazione” e “coscienza dell’osservazione” – si sviluppò nel 1957 tra gli allora amici Jung e Pauli, portando a una rottura che venne superata soltanto tempo dopo, nel 1958, alcuni mesi prima della morte di Pauli.
Sintentizzando al massimo – ho letto soltanto la notizia su questo fatto, che non riportava eccessive informazioni sul contenuto – Jung diceva che il “pensiero” non aveva a che vedere col secondo principio della termodinamica, Pauli tutto il contrario.
Siccome Jung non era fesso, è possibile che lui considerasse l'”emergenza” pensiero, nella sua forma, poiché ha sempre affermato, e su questo ha fondato tutta la sua opera, che la psiche è un fatto energico.
Ma allora, Pauli, come vede l'”emergenza”?
scusate: la psiche è un fatto “energetico”
“…Jung non era fesso…”.
affermazione temeraria e in ogni caso da dimostrare.
forse chi l’ha scritta non è mai stato in analisi junghiana.
e pure da uno bravo.
ma dai tash…
rileggendo: nel mio intervento 28.03, 10:27
“lunghezza d’onda” è “funzione d’onda”
@topo gigio, va bene l’esempio del triangolo con l’ipotenusa a scaletta: se il cateto è n allora l’area del triangolo con la scaletta è n(n+1)/2, mentre l’area del triangolo con gli scalini “tagliati” è n n/2, avanza n/2 che è appunto l’area degli scalini tagliati. La cosa interessante dell’esempio è che, se si mantiene costante la misura del cateto del triangolo e si aumenta a piacere il numero degli scalini, l’eccedenza diminuisce a piacere. “Al limite” l’eccedenza è per l’appunto nulla; il ché però non ha molte affinità col cosiddetto paradosso, se non per la presenza dell’idea di limite, che peraltro è la base di tutta l’analisi.
@liviobo: quello dell’anatra/coniglio non è minimamenteun paradosso; è un problema di Gestalt, e cioè delle capacità e modalità di percezione del nostro bizzarro cervello.
@l’ignorante ecc.: il problema di applicare la meccanica quantistica a un oggetto macroscopico, la pentola o la freccia o altro, è terrificante e non risolto neppure minimamente; non si può dire alcunché di ragionevole su quando si fa un osservazione su un sistema che contiene un numero dell’ordine del numero di Avogadro di oggetti (particelle elementari). O meglio si può dire solo quello che insegna, e con successo, la fisica classica.
Aggiungo en passant che la tesi di Wigner sulla supposta “irragionevole efficacia della matematica nelle scienze della natura” è certo suggestiva, ma non tiene conto dell’aspetto evolutivo; ovvero, semplificando al massimo: la matematica si è sviluppata nel modo che conosciamo attraverso un processo di accurato e graduale adattamento di quanto veniva escogitato dal pensiero alla realtà concreta.
no, Tash, Jung non era fesso: testimone Wolfgang Pauli, fisico teorico militante tra i più brillanti del Novecento. E testimone il loro interessantissimo carteggio (di cui tempo fa già si parlò qui in qualche commento).
mah, ho il timore che le posizioni siano troppo lontane per tentare una confutazione, già di per sè indaginosissima. l’anatra-lepre non sarebbe un paradosso percettivo, come quelli di Escher a tanti altri? perchè? e zenone non tentava forse di esemplificare la visione unitaria e atemporale dell’essere parmenidea? ecc. ecc. a ma pare che sparz ed altri che non posso non definire scientisti (senza voler fare del debolismo) se la cavino molto ingenuamente e comodamente relegando nello spazio del “bizzarro” , del “terrificante” e via dicendo tutto ciò che non gli torna: in realtà quelle bizzarrie pregiudicano, corrompono e più sostanzialmente costituiscono tutta la nostra logica. i paradossi, che gli scientisti di ogni generazione si illudono di aver risolto, risolti e dunque irrisolti eternamente, sono semploicemente le faglie spalancate sugli abissi “bizzarri”. dovrei argomentare sulla questione specifica? certo, ma data la scarsezza di presupposti comuni, ci vorrebbe un libro…
saluto con stima e perplessità
Secondo me quando ciò che il pensiero escogita viene adattato alla realtà concreta si forma una eccedenza (gli scalini tagliati); allo stesso modo, l’affermazione formulata dal pensiero di Zenone (non raggiungerà mai…), verificata nella realtà concreta eccede (in più o in meno – non ha importanza).
Il pensiero di una figura geometrica è vero; la realizzazione di una figura geometrica perfettamente rispondente, nella realtà concreta, all’idea non è realizzabile. Sono vere entrambi, l’idea e la figura reali, come sono vere le esposizioni del paradosso: 1. Non raggiungerà mai la tartaruga; 2. Raggiungerà la tartaruga dopo tot spazio in tot tempo.
L’ipotesi 1 è vera, perché il pensiero la può escogitare e se si può pensare nel pensiero vuol dire che da qualche parte è possibile. La 2 è vera perché chiunque anche senza misurazioni la può verificare con l’esperienza diretta. Quindi, se il mio ragionamento fin qui è corretto, la misurazione del paradosso nella realtà concreta dovrà dare un’eccedenza, sempre che il paradosso debba dare un resto, in questa ipotesi, per essere vero, e non si debba invece dire che è vero solo se non ammette il resto di eccedenza.
Nella realtà concreta, a pensarci bene, il paradosso non dà eccedenza, perché riguarda due affermazioni entrambe valide, che, guarda caso, si annullano a vicenda, come x=y; non come x=y+n (cioè Infinito=Materia+Resto), bensì come 0=0 (oppure Infinito=Reale; impossibile ai giorni nostri, almeno fino alla fine dei tempi).
Se non c’è resto, il paradosso è vero.
Topo G.
Casualmente – mentre leggo un libro che niente ha a che vedere con Zenone – vengo rimandato all’Iliade.
Non ricordavo certi particolari.
La domanda che mi pongo ora è questa: sono stati questi versi ad ispirare Zenone nella scelta delle figure con cui rivestire il suo paradosso? Infatti, non c’è soltanto il “pie’ veloce” Achille, ma anche “colui che non raggiunge”.
Iliade, XXII, 199 e sgg.:
“Come in sogno non si riesce a inseguire un fuggente
ché né l’uno riesce a scampare né l’altro a raggiungerlo,
così né Achille riusciva a raggiungere Ettore con la corsa,
né Ettore a sottrarglisi.”
Mi sembra appropriato scrivere qui il dettaglio dei miei commenti di questo post, opportunamente ordinati.
(topo Gigio/TG Honeylemon Buenasorte/evo)
Una teoria dell’eccedenza
Esiste una risultanza eccedente quando una misura infinita si porta ad una misura reale, dove l’eccesso è quello di una misura materiale.
Si può considerare la somma dei numeri da uno a cento, e la formula ad essa relativa, in relazione a una somma di quadrati da uno a cento, e vedere che c’è questa eccedenza nel contesto della materia; si può quindi dire che l’infinito genera l’eccedenza della materia.
Infinito = Materia + Resto
L’eccedenza è il resto. L’infinito meno il resto è uguale alla materia. Per astrazione, faccio questo ragionamento: l’infinito genera la materia, ma in questa operazione si forma una eccedenza, e questa eccedenza è il resto. Molto semplicemente, se abbiamo un infinito e lo “mettiamo” nella materia (materia quoziente) dobbiamo avere una eccedenza (resto).
Questo per contraddire coloro che credono alla materia come fabbrica di pensiero.
L’eccedenza non è il pensiero. L’eccedenza è l’amore. Una somma infinita che si fa rientrare in un quoziente di materia produce (scrivo “produce” perché non so cosa altro scrivere) un resto; questo è verificabile, per esempio, con la semplice formula:
n(n + 1)/2
La formula matematica e la formula intuitiva non si contraddicono.
Ecco, nel dettaglio, l’idea:
b(h+1)/2
In questa formula, b è la base di un triangolo rettangolo, h è l’altezza e poniamo b=h, cioè il triangolo ha i cateti uguali.
L’altra formula, quella delle serie, è:
n(n+1)/2
A questo punto scrivo l’area del triangolo:
b(h)/2
Accosto a questa formula quella delle serie, opportunamente cambiati gli n con base e altezza di un triangolo.
Questa è l’eccedenza di cui parlavo.
Immaginiamo di costruire una piramide con quadrati di un centimetro per lato. Mettiamo dieci quadrati alla base, poi nove, poi otto, e via così fino alla sommità, in cui mettiamo un quadrato. Il totale dei quadrati della piramide risulta essere 55, vale a dire 10(10+1)/2.
In pratica, ho preso la misura della base, dieci quadrati, l’ho moltiplicata per l’altezza, dieci, ho aggiunto la base o l’altezza, dieci, e ho diviso per due. L’eccedenza che mi risulta è la metà della base o dell’altezza ed è una eccedenza rispetto al disegno di un triangolo, cioè tra l’area di un triangolo disegnato e l’area di un triangolo costruito con quadrati di lato 1 (per esempio, una piramide).
Posso usare dei cubi di lato 1, al posto di usare i quadrati, e il risultato è complesso.
La misura non reale, come l’area di un triangolo perfetto, cioè immaginario, quando viene portata nel concreto, cioè costruita per esempio con quadrati di lato 1, produce una eccedenza.
Ciò che è escogitato dal pensiero, quando è adattato alla realtà concreta genera una eccedenza. Una cosa che il pensiero può escogitare, se si può pensare nel pensiero, da qualche parte è possibile, e la cosa reale è vera, perché chiunque anche senza misurazioni la può verificare con l’esperienza diretta; così, per quanto sopra detto, misurando un’idea nella realtà concreta si trova una eccedenza.
sì, senti, ne ha già parlato Godel. In modo più elegante. Poi?
Scusa zio Dag, ammetto che non sono stato elegante. Ho raccolto questa idea sparsa per i post e mi è sembrato appropriato metterla di continuo nei commenti. Mi scusa ancora.