Chi ha paura delle formule? #1
di Antonio Sparzani
[finita è la festa indiana; qualche evento programmato per ieri pomeriggio è saltato perché ci eravamo fatti prendere la mano dall’entusiasmo e avevamo messo troppa carne al fuoco. Niente di male. Qui vi propino qualcosa di quello che avrei voluto dire nella chiacchierata prevista nel pomeriggio con Chiara Valerio su scienza e letteratura. a.s.]
In testa a tutto io metto questa frase, che traggo dal Brusio della lingua di Roland Barthes che già qui ho ampiamente citato ed elogiato:
Tra la scienza e la letteratura esiste infine un terzo margine che la scienza deve riconquistare: quello del piacere.
Voi che non praticate le cosiddette scienza esatte, cosa pensate quando vedete scritta sulla carta una formula matematica?
Il primo pensiero sarà forse di rigetto, andrà a ricordi di scuola, complicazioni, cose per specialisti, scritture criptiche inventate per comunicare dei segreti che non si vuole diventino troppo condivisi, strumenti di un sapere iniziatico, astrusità, enigmi, cabale. Comunque cose incomprensibili: “Ah, io di matematica non ho mai capito niente”.
Anche se pensate così, sarebbe molto bello che il vostro secondo pensiero non fosse quello di ritirarsi e rinunciare per sempre a capire questi enigmi, ma fosse invece quello di poter distruggere la loro natura di enigmi. Una bella opzione di onnipotenza: « io posso distruggere la loro natura di enigmi ». Se un enigma diventa noto a tutti allora non è più un enigma, perde la sua natura, diventa una banalità che san tutti, un segreto di Pulcinella. Se questo pensiero vi sfiora o addirittura vi abita, dategli spazio, è un ottimo segnale. Si può proseguire, si possono immaginare analogie.
Se non conosceste la lingua nella quale questo post è scritto, le sue pagine sarebbero per voi completamente misteriose, perfino strane, con tutti quei segnetti messi in fila e magari qualche figura altrettanto strana, e così certo appaiono ad un cinese anche assai colto che ignori l’alfabeto latino. Ma se invece siete dei parlanti nativi di questa lingua, se l’avete succhiata con il latte materno e ha formato il veicolo della vostra entrata nel mondo, o se anche non l’avete succhiata col latte materno ma l’avete imparata poi, tutti i segnetti diventano miracolosamente portatori di significato, fanno risuonare qualcosa nella vostra testa, i segnetti t-e-s-t-a messi assieme alludono, ne siete sicuri, a quella parte del vostro corpo, così come di quello di tutti i vostri simili, nella quale “sentite” agitarsi tanti processi, che chiamate emozioni, ragionamenti e via dicendo, tutti nomi a loro volta appartenenti a questa stessa lingua.
Se non avete mai studiato musica e guardate uno spartito, provate la stessa sensazione di completa estraneità, mentre anche qui, se qualcuno vi ha invece messo a parte di quest’altro codice, di questo nuovo modo di tradurre segnetti in cose che fanno risuonare la vostra testa, allora lo spartito di nuovo acquista vita, ne carpite i segreti, che più tali non sono, esso rimanda anzi a una successione di suoni dei quali potrete innamorarvi o che potrete rifiutare, ma certamente avrà perso la sua natura di enigma. Perché è stato inventato questo codice? Perché sarebbe stato molto complicato usare le parole del linguaggio naturale per descrivere una melodia: ad esempio, si cominci con la nota, chiamata do3, corrispondente a tot vibrazioni al secondo di una corda metallica, poi si suoni la nota che ha i 9/8 della sua frequenza e poi… e poi… . Certamente infattibile.

È stato necessario inventare dei simboli per quelle note, un modo per scriverle, usando l’altezza rispetto ad un rigo fatto di cinque linee parallele orizzontali come simbolo del valore della sua frequenza, e poi codificare le pause tra le note, la durata di ognuna di esse, il ritmo da seguire, eccetera, eccetera.
… formule … formule:
Che cosa hanno in comune una Ferrari e il censimento della popolazione nell’antica Roma? Non molto, sembrerebbe, salvo che c’è una stessa parola che è implicata in entrambe. Nell’antica Roma, due millenni prima dell’epoca delle Ferrari, Tito Livio, storico di età augustea, scrisse un’opera immensa, cui si conviene di dare il titolo Ab urbe condita – dalla fondazione della città–per–eccellenza – un’opera che in 142 libri ripercorreva, con partecipazione e devozione intense per le sorti di Roma, la sua storia dalla fondazione all’inizio dell’impero, il tempo di Augusto. Mentre narra degli avvenimenti – in tempo di pace – della repubblica, Livio ha occasione di segnalare l’origine di un istituto importante nella storia di Roma, quello della censura che non designa, in quest’epoca, quel che oggi normalmente s’intende con questa parola (anche se non ne è poi così lontana, e forse tutto è cominciato da qui …), ma l’operazione di censire la popolazione, e censire significa, così ci racconta Livio, qualcosa di più che semplicemente contare e sapere nomi e domicili dei cittadini:
«In questo medesimo anno ebbe principio la censura, istituto che ebbe piccolo esordio, ma che acquistò di poi sì grande incremento. Ché il regolamento dei costumi e della disciplina Romana fu nelle mani del nuovo magistrato, ed il Senato e le centurie dei cavalieri ebbero il discernimento del loro onore o disonore in suo potere; e l’ispezione dei luoghi pubblici e privati, le rendite del popolo romano, furono al suo cenno ed arbitrio.» 1
Dunque un censimento non proprio neutrale, a quanto dice Livio: il potere del magistrato sembra andare oltre la mera registrazione dei cittadini; ma poiché, continua Livio, mentre diventava urgente eseguire questa operazione, i consoli avevano altre faccende più importanti da seguire,
«fu presentata al Senato una memoria, nella quale si faceva presente che quella operazione, faticosa e poco consolare, aveva bisogno di un magistrato speciale, dal quale dipendessero gli scribi, i custodi e la cura dei registri, e che regolasse a suo modo la formula del censimento [cui arbitrium formulæ censendi subiceretur]» 2
È proprio la parola latina formula, diminutivo di forma ma con un evidente slittamento di significato,» che fa la sua comparsa, nel senso di insieme di regole enunciate (stavo per scrivere “formulate”) con precisione, da seguire nell’esecuzione del censimento. Insieme di regole, dunque, purché ben precisate e non soggette ad ambiguità; prescrizioni chiare e distinte.
E la Ferrari non è, forse, per antonomasia, una macchina di “formula 1”? Anche qui la stessa parola, e usata, si noti, in un senso molto simile: l’insieme di regole cui è soggetta una certa categoria di automobili per poter partecipare a un ben preciso tipo di gare.
E poi c’è la formula di governo, un insieme di regole, frutto di delicati equilibri ed alchimie, dalle quali è costituita quella che l’orrido politichese chiama “la compagine ministeriale”. O la formula, spesso riservata, di una crema di bellezza, le regole ferree – e commercialmente segrete – con le quali deve essere composta quella crema, per poter avere quel marchio e quel nome.
Su questa strada ci si avvicina ovviamente alla formula chimica di un composto, quell’insieme di simboli, che funzionano secondo precise regole internazionalmente stabilite – N sta per azoto, C per carbonio, Sb per antimonio, ecc. – e che vanno combinati in modo da esprimere esattamente quali elementi e in quali proporzioni formano il dato composto;
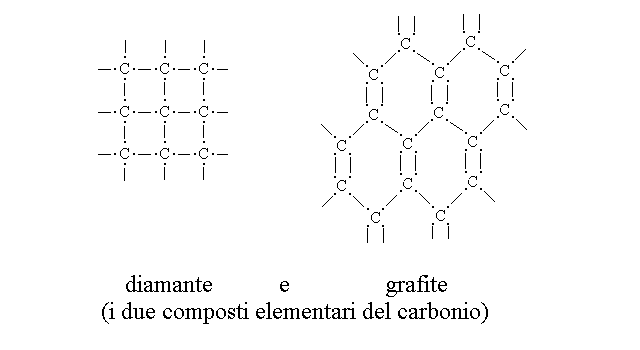
H2O, la formula dell’acqua, ci dà una informazione precisa su quali siano i costituenti elementari dell’acqua: ogni molecola, minima quantità d’acqua che ne conserva le proprietà, è costruita con due atomi di idrogeno e uno di ossigeno. Non è naturalmente una informazione ancora completa su come l’acqua è fatta (problematica in verità non facilissima neppure per i chimici provetti), però fornisce una informazione precisa, per quanto parziale, su un aspetto dell’acqua.
Fino ad arrivare alla formula fisica, o, in cima alla scala, alla formula matematica.
La matematica e tutto quanto le sta attorno, di formale, di iniziatico, di cabalistico, non è che un altro codice che è stato inventato per far fronte ad altre necessità. A cominciare da due: la necessità di contare, da una parte, e quella di misurare la terra dall’altra. Ma, si obietterà, da queste esigenze elementari – che risalgono alle antiche civiltà di cui si ha qualche documento – al castello gigantesco della matematica e della fisica contemporanea, c’è un vero abisso. Non riesco certo qui a rispondere brevemente alla domanda che chiede come ha potuto complicarsi in un modo così profondo un tale codice, risposta che richiederebbe un mucchio di analisi storiche specialistiche, però posso far notare, eseguendo un po’ una mossa di lato, come una delle espressioni più naturali e vitali della cultura umana, la letteratura, ha fatto i conti (metafora certamente adatta a questo scopo) con la matematica. In vari modi, un po’ ignorandola, un po’ esorcizzandola, o ammirandola da lontano, o trattandola con leggerezza e allegria. Un modo è quello di Hermann Broch che nel romanzo L’incognita scrive:
«Vede, – disse Kapperbrunn – la matematica è una sorta di atto disperato dello spirito umano… in sé e per sé non ci serve per niente, ma è una specie di isola dell’onestà, e per questo le voglio bene.»
Un altro è quello che usa Penelope Fitzgerald, quando, nel suo romanzo Il fiore azzurro nel quale ricostruisce la vita di Friedrich von Hardenberg, alias Novalis, fa dire ad uno dei suoi personaggi:
«l’algebra, come il laudano, attutisce il dolore» 3
E un altro ancora è quello contenuto nel secondo dei Canti di Maldoror, stupefacente scritto del conte di Lautréamont, pseudonimo di Isidore-Lucien Ducasse, maledetto tra gli scrittori maledetti della seconda metà dell’Ottocento francese:
«O matematiche severe, non vi ho dimenticate da quando le vostre sapienti lezioni, più dolci del miele, filtrarono dentro il mio cuore come un’onda rinfrescante. Istintivamente aspiravo, fin dalla culla, a bere alla vostra fonte, più antica del sole, e ancora continuo a calcare il vestibolo sacro del vostro tempio solenne, io, il più fedele tra i vostri iniziati. C’era del vago nella mia mente, un non so che, spesso come il fumo; ma io seppi valicare religiosamente i gradini che portano al vostro altare, e voi avete dissipato questo velo oscuro, come il vento scaccia la procellaria. Al suo posto voi avete messo un’estrema freddezza, una prudenza consumata e una logica implacabile.» 4
Nella prossima puntata un discorso più centrato sulla matematica e le sue formule.



Grazie per questo testo magnifico. Mi sembra parole per consolare un cuore infelice in matematico. Ho passato anni a scuola a non decifrare questa lingua, per me fredda e inquietante. Non ho visto la bellezza di questa lingua e non ho capito la passione che possia creare. Mi sentivo un viggiatore lunario sbarcato sur una terra arida, incomprehensibile. la solo lingua che amo è quella delle parole, un amore carnale e affetivo, quella della voce madre. Non ho mai sentito piacere davanti a una scrittura: il mio cervello si corruga, cerca una soluzione invano, si urta a un ostacolo. Nessuna matiere come la matematica non mi ha fatto capire come la mia intelligenza era limitata. Per sentire il piacere e la sensibilità ( se fosse una sensibilità in matematica) si deve prima impare la base. Matematica e macchine mi spaventano.
viaggiatore : scrittura matematica bien sûr!
Ho una storia (che per alcuni e’ anche una scusa) che credo di condividere con molti. Quella di non aver saputo amare la matematica per via delle persone che hanno cercato d’insegnarmela, ahime’.
Grazie per aver strappato il velo di maya, Antonio…
A me è sempre piaciuta la frase di Majakovschi che chi dice di non capire la poesia è come uno che si vanti di non capire la matematica.
“risposta che richiederebbe un mucchio di analisi storiche specialistiche”.
ecco.
nel momento in cui il pezzo poteva staccarsi dalla genericità e cominciare a mordere i problemi in chiave divulgativa, ti comporti esattamente come tutti i matematici, tipo: chettelodicoaffare? tanto non lo capisci. non sei uno specialista.
una (nuova) formula :
poesia = prosa -a -b -c
Piu’ che attutire il dolore la matematica addomestica al vero. Cio’ che la rende una dottrina comunemente accettata da tutti e da tutti riconosciuta come forma insostituibile del sapere, e’ il suo intento assolutizzante. Che e’ al tempo stesso un fortalizio della logica del controllo e un programma falsamente rassicurante. La matematica seduce perche’ mira a rappresentare il mondo come un’entita’ logica, determinata, compresa. Ma il mondo naturale non e ne’ logico, ne’ determinato, ne’ compreso.
A sua volta la letteratura fa i conti con la matematica nel senso che il numero si propone di conferire unidirezionalita’ al percorso di oggettivazione della parola cristallizzata graficamente. Lo scritto, infatti, sebbene riduca l’esperienza del parlato in una struttura chiusa fatta di segni, linee, direzioni da seguire e ortografia, non e’ ancora in grado di assurgere a forma di verita’. Condiziona certamente il lettore senza offrire alcuna possibilita’ immediata di confronto, ma rimane pur sempre circoscritto nell’ambito delle opinioni. Nessuno scritto e’ assolutamente vero. Anche i comandamenti di Dio si prestano all’interpretazione. Il numero sfonda questa barriera di opinabilita’ e trasforma l’esperienza della comunicazione in esternazione di verita’. Chi ha mai potuto negare che 2+2 faccia 4? Da qui l’assunto che il numero, prodotto operativo della scrittura, non potrebbe esistere senza di essa. La letteratura dunque, non ha ignorato o esorcizzato la matematica, l’ha creata.
Che sia proprio il linguaggio matematico la poesia della materia? Perchè no?
Contributo a definizione di poesia: (Da Rainero Gnoli, parlando di mantra e altro nel 1972) “…come espressioni linguistiche aconvenzionali, possono essere paragonati, da un lato ai gridi di animali, alle interiezioni o alle intonazioni della voce che, come essi, esprimono uno stato di coscenza indipendentemente dalle categorie logiche del pensiero e, dall’altro lato al linguaggio poetico, che sebbene si basi su un linguaggio pratico e convenzionale non si esaurisce tuttavia in esso, ma si accresce di un senso, di una risonanza nuova che, se coesiste col senso storico e letterale della parola e si esprime anzi attraverso esso, non può essere identificata con esso”.
per Brown: La letteratura ha creato anche le religioni (non solo quelle del libro) e quasi tutto il resto che esiste, o sbaglio?
trovo questo articolo bellissimo. Io, invece, la matematica l’ho sempre amata così come la letteratura. Ricordo un geniale docente che spiegava la matematica citando spesso dante, facendo degli incisi filosofici (di due ore) , fra una spiegazione e l’altra. fantastico
@ maurizio: non sbagli, la scrittura e’ il piu’ efficace strumento di asservimento degli individui, conseguenziale dunque l’invenzione di dio e della matematica. Anche Levi-Strauss non ha dubbi in proposito: “l’unico fenomeno che sembra sempre e comunque legato all’apparizione della scrittura e’ la costituzione di societa’ gerarchizzate, di societa’ di padroni e di schiavi, di societa’ che utilizzano una certa parte della loro popolazione per lavorare a profitto dell’altra parte”.
Gentile Brown fraintendi. Attravarso le parole, al canto, si può dare corpo a un pensiero religioso in forme più o meno avvincenti (spesso magnifiche, si pensi alle mitologie di Shiva o Dioniso, al Ramayana, al Mahabarata) e forse si tratta del meglio che l’uomo abbia saputo produrre dacché esiste, ma Dio in quanto tale non è una robetta che si possa confezionare con carta e penna. Senza la pretesa di corrompere un ateo, che nella sua religione immagino animato da fervore incrollabile, vorrei ricordare l’opinione del grande matematico, chimico, ingegnere e prete ortodosso Pavel Florenskij. Egli ammetteva tutte le difficoltà circa una qualsiasi dimostrazione razionale dell’esistenza di Dio, problema che peraltro espresso in questi termini risulta ovviamente di somma cretineria, ma sosteneva non fosse ammissibile che la quasi totalità degli uomini, compreso i più saggi, da tempo immemorabile potesse farsi preda di una bufala di questa portata. Dunque, il semplice rispetto di tali uomini dovrebbe mettere sull’avviso circa la complessità e la serietà del problema. Se poi uno nasce con l’anima di schiavo non ha bisogno neppure della fede dei preti per esprimere la propia natura: infatti il conformismo e l’asineria pubblica danno oggi sfarzosa prova di sè in infiniti altri modi. I Pigmei e gli Aborigeni solo apparentemente non sono società gerarchizzate perché al loro interno si riconoscono invece chiaramente i ruoli e le funzioni guerriera, sacerdotale/sciamanica, e produttiva. Se non usano la scrittura, questo non significa che non posseggano una ricchissima letteratura orale, una complicatissima riserva di miti e dei principi fondatori e generatori schiettamente e puramente metafisici. La società gerarchizzata nuoce quando la piramide si rovescia e i delinquenti si trovano sul suo spaziosissimo vertice. Per sfruttare un uomo non sono necessari procedimenti di scrittura, di regola è sufficiente un bastone. Di Florenskij consiglio vivamente la lettura: “Le porte regali”, saggio sull’Icona e “La colonna e il fondamento della verità”, saggio di teodicea ortodossa.
mah, l’esistenza della matematica non mi pare abbia a che fare con l’esistenza di Dio, anche se probabilmente Gödel pensava diversamente. A Brown (“La matematica seduce perché mira a rappresentare il mondo come un’entità logica, determinata, compresa.”) vorrei dire che la matematica non vuole necessariamente rappresentare il mondo, ma sul come e sul perché di ciò tornerò nella seconda puntata. Così come tornerò su quello che lamenta Tash, che invito a pazientare un attimo; del resto su un tema come quello del costante complicarsi delle strutture matematiche mi darà atto che non si combina un’analisi seria in un post, tuttavia qualcosa da mordere lo troverà.
” Nessun limite a questa concatenazione, salvo ‘ il bordo di questo foglio di carta ‘ “. J. Kristeva, Semeiotikè, 1978, p. 158.
” Lo zero è due che sono uno “.